티스토리 뷰
2020/10/25 - [분류 전체보기] - optimizer 종합 banch mark ( 인공지능 기초 # 17)
가중치의 초기값 설정
가중치를 평균이 0, 표준편차가 1인 정규분포로 초기화할때의 각 층의 활성화값 분포
입력층 -> 첫번째 입력층 으로갈때 10000개의 변수가 생김 (입력층 100, 은닉층 100 = 100*100 =10000) 그 변수를 표준변차가 1인 정규분포를 따라서 선택을 하겠다는 뜻 아래 그래프는 sigmoid 함수를 적용한 데이터 1-layer의 데이터를 activations에 담아두고 [z] 출력 값 z를 다시 2-layer의 입력값으로 사용하는데 또 표준정규분포에 따라서 선택함 반복
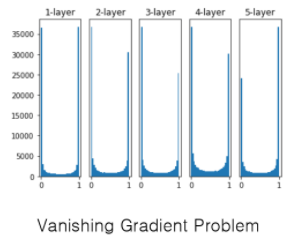
--> Vanishing Gradient Problem 이 일어나면, 학습이 거의 안이루어짐

굉장히 작은 미분계수 값을 계속 곱해나가게 되면 나중에는 너무작아져서 학습이 거의 안이루어짐 ,, 층을 깊게 쌓은 이유가 전혀 없어짐 굉장ㅎ ㅣ 심각한 문제 인공신경망의 두번째 겨울의 이유이기도 했습니다.
가중치를 평균이 0, 표준편차가 0.01인 정규분포로 초기화할때의 각층의 활성화값 분포 [표준편차가 0.01이라는건 값들이 거의 차이가 없다는뜻]
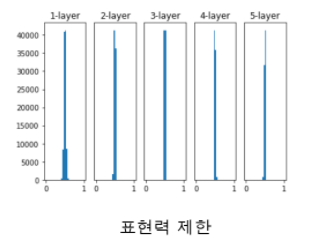
--> 표현력제한 : 완전 중심에 몰려있게됨 , 학습이 거의 안된거
첫번째 가중치 행렬의 각 행이 동일하고 두번째부터는 각 단계마다 가중치가 동일한 신경망을 생각해봅니다. 이는 1층부터 뉴런의 개수가 모두 1개인 신경망과 본질적으로 동일합니다.

뉴럴 네트워크가 실질적으로 엄청나게 단순한 뉴럴 네트워크가 되어서 데이터의 정보를 담을 슬롯이 부족해지는 문제점이 있다.
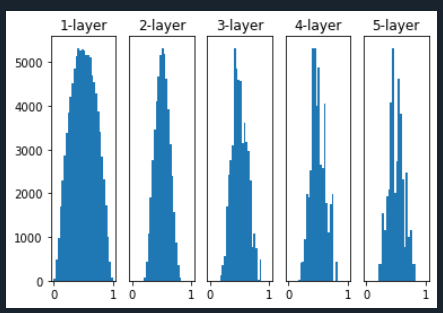
가중치를 평균이 0, 표준편차가 np.sqrt(1.0인 정규분포로 초기화할때의 각층의 활성화값 분포
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))#
def ReLU(x):
return np.maximum(0, x)#
def tanh(x):#하이퍼붤리 탄젠트 ,, 자연어 처리에서 많이 씀
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 1000개의 데이터 1000*100행렬을 만든다
node_num = 100 # 각 은닉층의 노드(뉴런) 수
hidden_layer_size = 5 # 은닉층이 5개
activations = {} # 이곳에 활성화 결과를 저장
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 초깃값을 다양하게 바꿔가며 실험해보자!
w = np.random.randn(node_num, node_num) * 1
# w = np.random.randn(node_num, node_num) * 0.01
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
# 활성화 함수도 바꿔가며 실험해보자!
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z
# 히스토그램 그리기
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
if i != 0: plt.yticks([], []) # 0이아니면 y택 없애라
# plt.xlim(0.1, 1)
# plt.ylim(0, 7000)
plt.hist(a.flatten(), 30, range=(0,1)) 0-1까지를 30등분해서 그려라
plt.show()
( 우리가 뉴럴 네트워크를 학습을 시작하기 전에 weight를 랜덤하게 설정을 하는데 랜덤하게 설정을 할 때 표준편차를 너무작게 잡으면 아무리 뉴럴 네트워크를 복잡하게 설계했어도 실질적으로 지극히 단순한 뉴럴네트워크와 본질적으로 같아집니다. 그래서 데이터의 정보를 담을 수 있는 파라미터의 숫자가 너무 적어져서 표현력 제한이라고 부릅니다. )
weight를 큰 표준편차로 랜덤하게 설정하고 학습을 시작하게 되면 Vanishing Gradient Problem에 부딪히게 됩니다. 밑 층으로 내려 갈 수록 점점 사라져가는... 아래층에선 하는 의미가 없어지는 큰 문제가 생깁니다.
즉 가중치의 초기값을 너무 크지도 너무 작지도 않게 잘 설정을 해야합니다.

Xavier initialization , 2/n_in + n_out = 1/n_in+n_out/2 입니다.
학습을 시작하기 전에 입력뉴런의 갯수와 출력뉴런의 갯수를 평균한것의 역수를 가지는 정규분포를 따라서 랜덤하게 학습을 시키면 결과가 좋습니다.
LeCun initialization , 1/n_in 입니다.
학습을 시작하기 전에 입력뉴런의 갯수의 역수를 가지는 정규분포를 따라서 랜덤하게 학습 시키면 결과가 좋다고 합니다. 자비에 초기값보다 간단한 형태입니다.
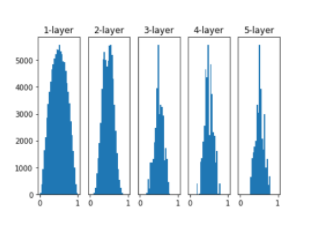
#w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
루트(1/입력뉴런)
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))#
def ReLU(x):
return np.maximum(0, x)#
def tanh(x):#하이퍼붤리 탄젠트 ,, 자연어 처리에서 많이 씀
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 1000개의 데이터 1000*100행렬을 만든다
node_num = 100 # 각 은닉층의 노드(뉴런) 수
hidden_layer_size = 10 # 은닉층이 10개
activations = {} # 이곳에 활성화 결과를 저장
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
a = np.dot(x, w)
# 활성화 함수도 바꿔가며 실험해보자!
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z
# 히스토그램 그리기
for i, a in activations.items():
plt.subplot(2, len(activations)/2, i+1) #len(activations) ==10
plt.title(str(i+1) + "-layer")
if i%5 != 0: plt.yticks([], [])#나눈 나머지가 0이아니면 (0일때와 5일때 10일때 뺴고) y택이 살아있어라
if i<5 : plt.xticks([], [])# i가 5보다 작으면 x틱 지워라 5 6 7 8 9 는 살아있음
# plt.xlim(0.1, 1)
# plt.ylim(0, 7000)
plt.hist(a.flatten(), 30, range=(0,1)) 0-1까지를 30등분해서 그려라
plt.show()
He 초기값

활성화함수를 시그모이드를 잡았을 때는 자비에를 쓰고 렐루를 잡았을 때는 헤를 씁니다.

렐루 함수를 사용할 때 자비에를 쓰면 층이 지날수록 왼쪽으로 치우치지만 He를 쓰면 일정한걸 볼 수 있습니다.
자비에(LeCun이지만 책에서는 자비에를 LeCun과 동일시 함) :
np.sqrt(1.0 / node_num)헤 :
np.sqrt(2.0 / node_num)
초기값을 0.01로 했을때와 Xavier , He를 썻을때입니다. 0.01은 거의 학습이 되지 않는것을 볼 수 있습니다.
1로도 해보았는데 값이 큰 상태에서 내려오질않아서 결과가 나오지 않아 0.5로 설정해 보았습니다.
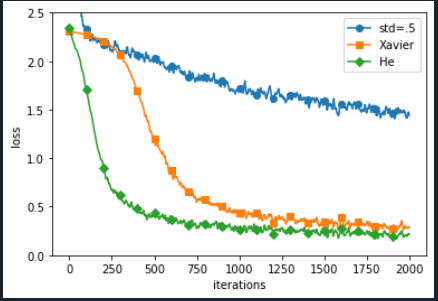
초기값의 설정이 학습에 엄청난 영향을 미치는것을 볼 수 있습니다.
'Study > 인공지능' 카테고리의 다른 글
| Overfitting [과적합] ( 인공지능 기초 #20 ) (0) | 2020.10.26 |
|---|---|
| 배치 정규화 ( 인공지능 기초 #19 ) (0) | 2020.10.26 |
| optimizer 종합 banch mark ( 인공지능 기초 # 17) (0) | 2020.10.25 |
| Optimizer : Adam ( 인공지능 기초 # 16 ) (0) | 2020.10.25 |
| Optimizer : AdaGrad, RMSprop ( 인공지능 기초 # 15 ) (0) | 2020.10.24 |

