티스토리 뷰
저번 글에서 퍼셉트론의 정의를 알아보았습니다.
2020/09/13 - [Study/인공지능] - 퍼셉트론, 뉴런 네트워크의 모방 ( 인공지능 기초 #1 )
퍼셉트론, 뉴런 네트워크의 모방 ( 인공지능 기초 #1 )
퍼셉트론은 신경망(딥러닝)의 기원이 되는 알고리즘 입니다. 퍼셉트론의 구조를 배우면 신경망과 딥러닝의 기초를 닦을 수 있습니다. 인공신경망(artificial neural network 아티피셜 뉴럴 네트워크)
15051015.tistory.com
이번에는 퍼셉트론으로 논리 회로를 구현해 보겠습니다.
1. AND 게이트

이 AND 게이트를 퍼셉트론으로 표현하고 싶습니다. 이를 위해 w1, w2, Θ (임계점)의 값을 정해야 합니다.
그럼 어떤 값으로 설정을 하면 위의 AND 게이트를 충족하는 퍼셉트론을 만들 수 있을까요?
답은 매우 여러개가 나올 수 있습니다. 현재 제가 공부하고 있는 책에서는 W1, W2 : 0.5 임계점 : 0.7로 잡았습니다.

0.5 * 1 + 0.5 * 1 = 1 (true) , 0.5 * 1 + 0.5 * 0 = 0.5 (false) , 0*0.5 + 0*0.5 = 0 (false)
임계점 0.7과 가중치 0.5로 설정한 뒤 [x1,x2] : [1,1] [1,0] [0,1] [0,0] 을 각각 대입하였을 때
AND 게이트와 같은 값이 나오게 됩니다.
2. NAND 게이트

이 NAND 게이트를 퍼셉트론으로 표현하고 싶으면 w1,w2 임계점을 어떻게 잡아야 할까요?
제가 공부한 책에서는 w1 ,w2 = -0.5, 임계점 = -0.7로 설정하였습니다.
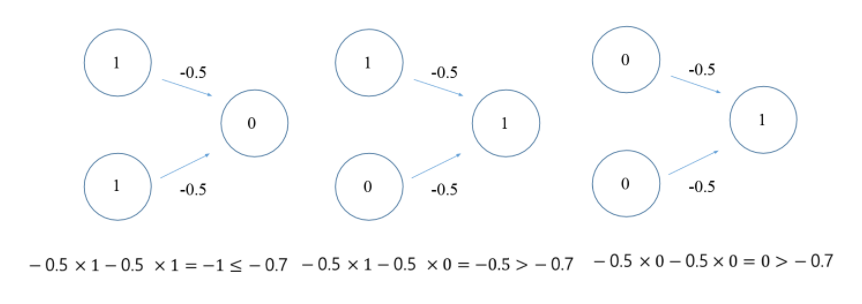
-0.5 * 1 + -0.5 * 1 = -1 (false) , -0.5 * 1 + -0.5 * 0 = -0.5 (true) , 0*-0.5 + 0*-0.5 = 0 (true)
임계점 -0.7과 가중치 -0.5로 설정한 뒤 [x1,x2] : [1,1] [1,0] [0,1] [0,0] 을 각각 대입하였을 때
NAND 게이트와 같은 값이 나오게 됩니다.
3. OR 게이트

이 OR 게이트를 퍼셉트론으로 표현하고 싶으면 w1,w2 임계점을 어떻게 잡아야 할까요?
제가 공부한 책에서는 w1 ,w2 = 0.5, 임계점 = 0.2로 설정하였습니다.

0.5 * 1 + 0.5 * 1 = 1 (true) , 0.5 * 1 + 0.5 * 0 = 0.5 (true) , 0*0.5 + 0*0.5 = 0 (false)
임계점 0.2과 가중치 0.5로 설정한 뒤 [x1,x2] : [1,1] [1,0] [0,1] [0,0] 을 각각 대입하였을 때
OR 게이트와 같은 값이 나오게 됩니다.
OR는 AND보다 true가 나오기 쉬운 게이트입니다. 즉 임계점을 AND에서 0.7이었던 것과 다르게 0.2로 설정해줍니다.
우리가 설정한 가중치와 임계점은 엄청나게 많은 경우가 있을 수 있습니다.
다음은 한개의 퍼셉트론으로는 만들 수 없는 게이트를 만들어 보도록 하겠습니다.
'Study > 인공지능' 카테고리의 다른 글
| 확률 벡터 (Softmax 변환) overflow 대책 증명 ( 인공지능 기초 #5-2) (0) | 2020.09.17 |
|---|---|
| 3층 인공신경망 ( 퍼셉트론과 활성화 함수의 결합 ) ( 인공지능 기초 #5-1) (1) | 2020.09.16 |
| Heaviside 함수 Sigmoid함수 ReLU 함수, 신경망과 활성화 함수 ( 인공지능 기초 #4 ) (0) | 2020.09.15 |
| 다층 퍼셉트론 XOR 논리회로 표현하기 , 단층으로 안되는 이유 ( 인공지능 기초 #3 ) (0) | 2020.09.14 |
| 퍼셉트론, 뉴런 네트워크의 모방 ( 인공지능 기초 #1 ) (0) | 2020.09.13 |
